读书笔记-算法-第一章

配套网站:https://algs4.cs.princeton.edu/home/
第一章 基础
- 无论在任何应用领域,精心设计的算法都是解决大型问题最有效的方法
- 我们把描述和实现算法所用到的语言特性、软件库和操作系统特性总称为基础编程模型
- java程序的基本语法,同时也是多数程序语言的通用语法
- 原始数据类型:它们在计算机程序中精确地定义整数、浮点数和布尔值等。它们的定义包括取值范围和能够对相应的值进行的操作,它们能够被组合为类似于数学公式定义的表达式。
- int 32位整数(2^31=2147483648)
- 在java中int可表示的范围为(-2147483648——2147483647),2147483648会溢出变为-2147483648,因此Math.abs(-2147483648)=-214783648
- double 64位双精度实数
- 布尔型 true or false
- string 字符串
- long 64位整数
- short 16位整数(2^15=32768)
- char 16位字符
- byte 8位整数(2^7=128)
- float 32位单精度实数
- int 32位整数(2^31=2147483648)
- 语句:语句通过创建变量并对其赋值、控制运行流程或者引发副作用来进行计算。我们会使用六种语句:声明、赋值、条件、循环、调用和返回
- java是一种强类型语言,编译器会检查类型一致性
- 数组:数组是多个同种数据类型的值的集合
- 静态方法:静态方法可以封装并重用代码,使我们可以用独立的模块开发程序
- 字符串:字符串是一连串的字符,Java内置了对它们的一些操作
- 标准输入/输出:标准输入输出是程序与外界联系的桥梁
- 数据抽象:数据抽象封装和重用代码,使我们可以定义非原始数据类型,进而支持面向对象编程
- 原始数据类型:它们在计算机程序中精确地定义整数、浮点数和布尔值等。它们的定义包括取值范围和能够对相应的值进行的操作,它们能够被组合为类似于数学公式定义的表达式。
- 不同程序语言的运算符计算优先级会有不同,因此通常情况下用括号来进行优先级的改变
- 方法的性质
- 方法的参数按值传递
- 调用方法时传递对象名也是值传递,意味着传递的是对象的别名,也就是对象的引用地址,所以在方法内修改其内容也会影响原始值
- 方法名可以重载
- 方法只能返回一个值,但是可以包含多个返回语句
- 方法可以产生副作用:在本书中,返回值是void的方法就是副作用
- 方法的参数按值传递
- 递归原则
- 递归总是在第一行就要包含一个包含return的条件语句
- 递归总是尝试先解决一个更小的问题
- 递归的父问题和子问题之间不应该有交集
- API的目的是将调用和实现分离
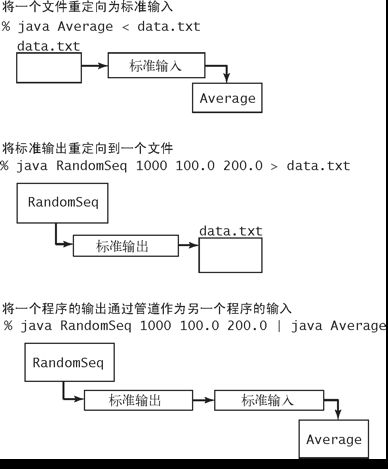
- 重定向和管道输入
- Java表达式1/0和1.0/0.0的值是什么
- 第一个表达式会产生一个运行时除以零异常(它会终止程序,因为这个值是未定义的);第二个表达式的值是Infinity(无穷大)。
- 为什么数组的起始索引是0而不是1
- 这个习惯来源于机器语言,那时要计算一个数组元素的地址需要将数组的起始地址加上该元素的索引。将起始索引设为1要么会浪费数组的第一个元素的空间,要么会花费额外的时间来将索引减1
- 每次使用new来创建一个对象时,系统都会
- 为新的对象分配内存空间
- 调用构造函数初始化对象中的值
- 返回该对象的一个引用
- 为什么要区别原始数据类型和引用类型?为什么不只用引用类型
- 因为性能。Java提供了Integer、Double等和原始数据类型对应的引用类型,以供希望忽略这些类型的区别的程序员使用。原始数据类型更接近计算机硬件所支持的数据类型,因此使用它们的程序比使用引用类型的程序运行得更快
- 指针是什么?
- 和Java的引用一样,可以把指针看做机器地址。在许多编程语言中,指针是一种原始数据类型,程序员可以用各种方法操作它。
- 但众所周知,指针的编程非常容易出错,因此需要精心设计指针类的操作以帮助程序员避免错误。Java将这种观点发挥到了极致(许多主流编程语言的设计者也赞同这种做法)。
- 在Java中,创建引用的方法只有一种(new),且改变引用的方法也只有一种(赋值语句)。也就是说,程序员能对引用进行的操作只有创建和复制。
- 在编程语言的行话里,Java的引用被称为安全指针,因为Java能够保证每个引用都会指向某种类型的对象(而且它能找出无用的对象并将其回收)。
- 栈用于带括号的运算符计算

- Java标准库中有栈和队列吗
- Java有一个内置的库,叫做java.util.Stack,但你需要栈的时候请不要使用它。
- 它新增了几个一般不属于栈的方法,例如获取第i个元素。它还允许从栈底添加元素(而非栈顶),所以它可以被当做队列使用
- java.util.Stack的API是宽接口的一个典型例子
- 算法分析
- 一个程序运行的总时间主要和两点有关
- 执行每条语句的耗时
- 执行每条语句的频率
- 常见的增长数量级函数
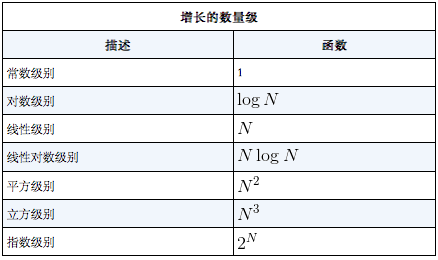
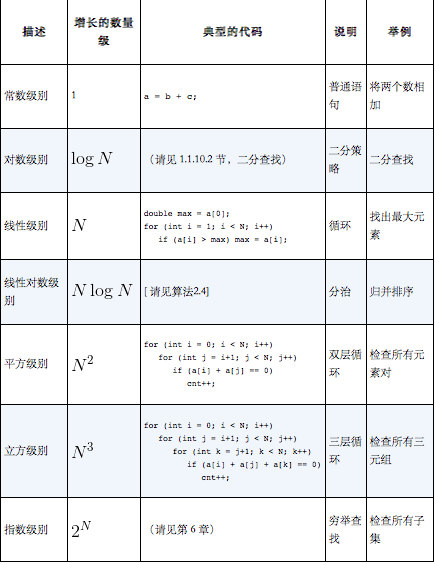
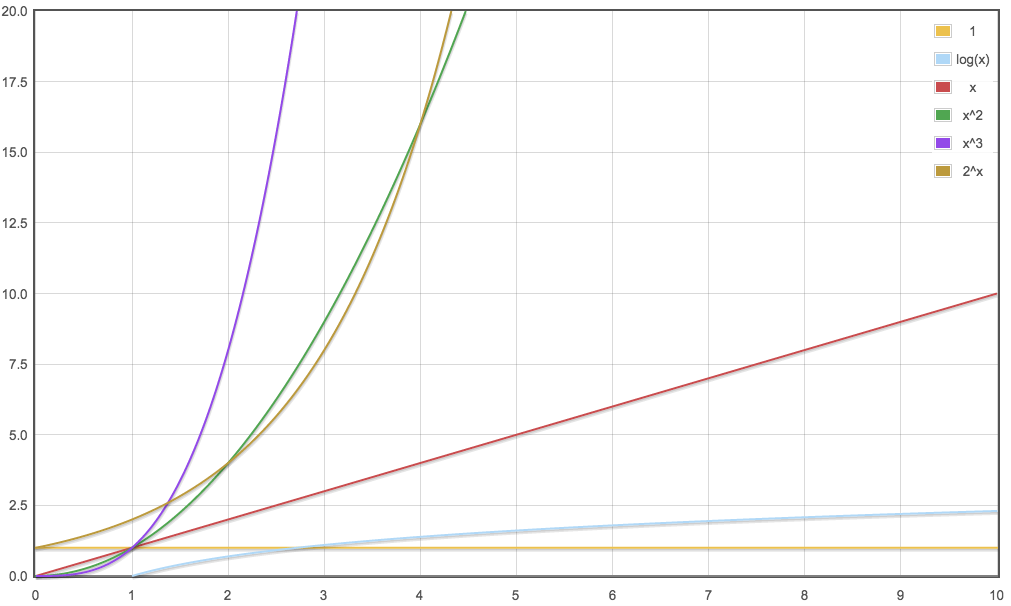
- 从增长率来看,效率排行是常数>logN>N>N^2>2^N>N^3
- 一个程序运行的总时间主要和两点有关
- 解决3-sum问题
- 即在给定的数组中找到和为0的三个数
- 解决2-sum问题
- 使用归并排序对数组进行排序,复杂度为NlogN
- 遍历数组,第一个数找到后使用二分查找在排序后的数组中获取相反数,时间复杂度为NlogN
- 因此整个2-sum问题的时间复杂度为logN
- 将解决2-sum问题的方法推广
- 使用归并排序对数组进行排序,复杂度为NlogN
- 遍历数组,但是这时,需要遍历两遍,相当于先把两个数相加后再用二分法去找数组中的相反数,因此时间复杂度为(N^2)*logN
- 这样3-sum的问题的时间复杂度为(N^2)*logN
- 可以看到,针对这样的问题,先排序一遍所需的成本在总成本中几乎可以忽略不计,而排序后可以使用二分法则可以将整个时间复杂度降一个量级

- 考虑数量级的注意事项
- 大常数,考虑数量级一般情况下不需要去考虑常数,如2N^2 + cN,通常情况下是看成N^2,然而如果某些情况下,c的值非常大,大到在具体业务场景中无法忽略的话,还是需要将常数考虑进去
- 非决定性的内循环
- 内循环是决定性因素的假设并不总是正确的
- 有些程序在内循环之外也有大量指令需要考虑
- 指令时间
- 每条指令执行所需的时间总是相同的假设并不总是正确的
- 例如,大多数现代计算机系统都会使用缓存技术来组织内存
- 系统因素
- Java只是争夺资源的众多应用程序之一,而且Java本身也有许多能够大大影响程序性能的选项和设置
- 某种垃圾收集器或是JIT编译器或是正在从因特网中进行的下载都可能极大地影响实验的结果
- 对输入的依赖
- 某些特殊值导致的运行时间的陡然差异不应该考虑进我们对于程序整体运行时间的评估
- 考虑最坏情况下对于性能的保证
- 引入随机化算法
- 需要模拟随机数的输入
- 考虑操作序列
- 即某些情况下,进行ABC操作和进行CBA操作的顺序可能也会对性能造成影响
- 均摊分析
- 提供性能保证的另一种方法是通过记录所有操作的总成本并除以操作总数来将成本均摊
- 速度太慢的程序和错误的程序一样无用
- union-find算法
- 问题的输入是一列整数对,其中每个整数都表示一个某种类型的对象,一对整数pq可以被理解为“p和q是相连的”
- 规则
- 自反性:p和p是相连的
- 对称性:如果p和q是相连的,那么q和p也是相连的
- 传递性:如果p和q是相连的且q和r是相连的,那么p和r也是相连的
- 动态连通性问题
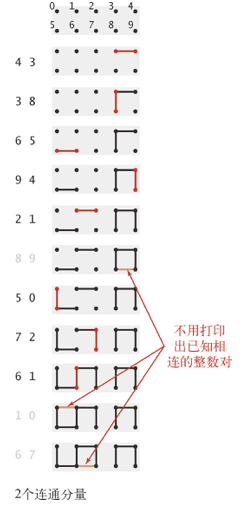
- 当程序从输入中读取了整数对pq时,如果已知的所有整数对都不能说明p和q是相连的,那么则将这一对整数写入到输出中
- 如果已知的数据可以说明p和q是相连的,那么程序应该忽略pq这对整数并继续处理输入中的下一对整数
- 比如没有连通数据时,输入1,3,将其连通,输出1-3;接下来再输入3,5,将其连通,输出3-5;这样在输出记录中,存在1-3-5的连通记录;此时,输入1,5,根据连通规则,1和5是连通的,所以忽略这对数据
- 用处
- 这个程序能够判定我们是否需要在p和q之间架设一条新的连接才能进行通信,或是我们可以通过已有的连接在两者之间建立通信线路
- 这些整数表示的可能是社交网络中的人,而整数对表示的是朋友关系
- 术语
- 将对象称为触点,将整数对称为连接,将等价类称为连通分量或是简称分量
- 实现方法
- 用一个以触点为索引的数组id[]作为基本数据结构来表示所有分量
- 定义四个基本API
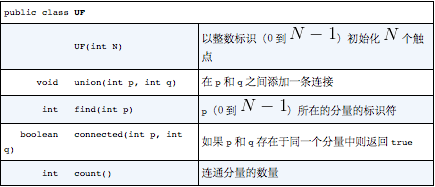
- quick-find算法
- connected(p,q)只需要判断id[p]==id[q]
- 我们需要遍历整个数组,将所有和id[p]相等的元素的值变为id[q]的值。我们也可以将所有和id[q]相等的元素的值变为id[p]的值——两者皆可
- 举例来说,1-3本来相连,则数组id[]中id[1]和id[3]的值相等,比如都等于1
- 这时需要连接另一对触点,比如5-6,数组id[]中id[5]和id[6]的值相等,比如都等于5
- 现在需要将3和5连接,此时遍历数组,找到与id[3]和id[5]的值相同的索引,即1和6,此时将索引1,3,5,6的值都改为1或者都改为5



- union方法包含三步,一步是find,找到各自对应的值,复杂度为O(1),第二步是遍历数组,复杂度为O(N),第三步是修改数组中的值,根据连通量的不同,可能需要1——N-1步
- 最差的情况下,只得到一个连通分量,如1-5的数组,最终连通分路只有一条1-2-3-4-5,其复杂度接近O(N^2)
- 两个数组连通每次都需要N+3步,即两次find为2步,遍历数组N步,改变值1步,2+N+1=N+3步
- 只有一个通路的情况下,数组中依次比较需要N-1步,如1-5的数组,步骤为1-2,2-3,3-4,4-5。
- 所以最终步骤为(N+3)*(N-1),时间复杂度记为O(N^2)
- 这个时间复杂度在数据量达到上亿的情况下显然效率过低,不予考虑
- quick-union算法
- 每个触点所对应的id[]元素都是同一个分量中的另一个触点的名称,称为链接

- 在数组被初始化之后,每个节点的链接都指向它自己
- 每次union之后节点都会指向某个父节点,id[i]的值除非是根节点,否则不会等于自身,因此代码中的find会一直追溯到父结点
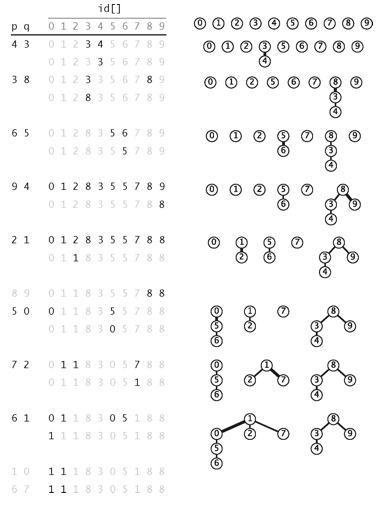
- 与quick-find相比,最明显的改变就是每次union的操作无需遍历数组,只需将子节点指向父节点即可,这个过程只需一步
- 相比之下,就要付出额外的成本去追溯父节点,这个过程最快1步,最慢需要N-1步
- 在最坏的情况下,所有的节点的链接都指向前一个节点,那么每次find都需要遍历之前的每个节点,总的find的步骤就是3+5+6+……+(2N-1)~N^2
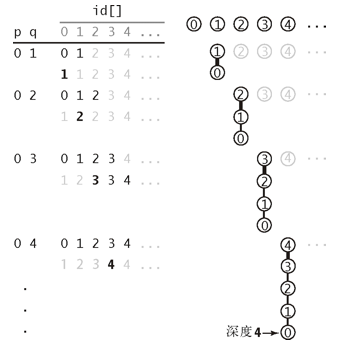
- 在一般情况下都会比quick-find更快,但是无法保证出现最坏情况下仍然是O(N^2)的时间复杂度
- 每个触点所对应的id[]元素都是同一个分量中的另一个触点的名称,称为链接
- 加权quick-union算法
- 记录每一棵树的大小并总是将较小的树连接到较大的树上
- 需要添加一个数组和一些代码来记录树中的节点数

- 对于N个触点,加权quickunion算法构造的森林中的任意节点的深度最多为lgN
- 多出来记录节点数量的数组并不会增加多少复杂度,只会在每次union中多出两步操作
- 使得find成本大大降低,随着数量级的提升,时间复杂度只会以lgN的数量级增长
- 路径压缩的加权quick-union算法
- 我们希望每个节点都直接链接到它的根节点上,但我们又不想像quickfind算法那样通过修改大量链接做到这一点
- 要实现路径压缩,只需要为find()添加一个循环,将在路径上遇到的所有节点都直接链接到根节点
- 我们所得到的结果是几乎完全扁平化的树,它和quickfind算法理想情况下所得到的树非常接近
- 是目前的最优解