第四章 图
- 无向图
- 定义
- 图是由一组顶点和一组能够将两个顶点相连的边组成的
- 边(edge)仅仅是两个顶点(vertex)之间的连接
- 一般使用0至V-1来表示一张含有V个顶点的图中的各个顶点
- 我们用v-w的记法来表示连接v和w的边,w-v是这条边的另一种表示方法
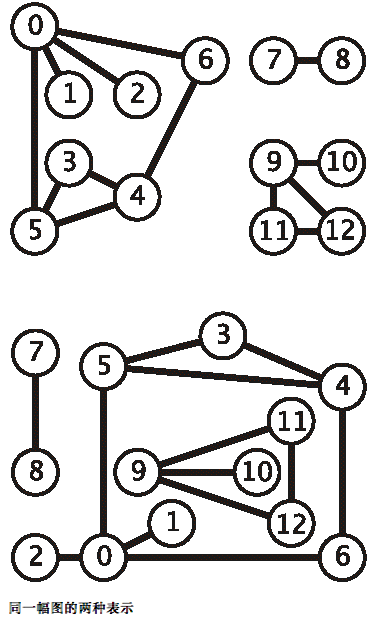
- 特殊的图
- 自环,即一条连接一个顶点和其自身的边
- 连接同一对顶点的两条边称为平行边
- 术语定义
- 当两个顶点通过一条边相连时,我们称这两个顶点是**相邻的**,并称这条边**依附于**这两个顶点
- 某个顶点的**度数**即为依附于它的边的总数。**子图**是由一幅图的所有边的一个子集(以及它们所依附的所有顶点)组成的图
- 在图中,**路径**是由边顺序连接的一系列顶点
- **简单路径**是一条没有重复顶点的路径
- **环**是一条至少含有一条边且起点和终点相同的路径
- **简单环**是一条(除了起点和终点必须相同之外)不含有重复顶点和边的环
- 路径或者环的**长度**为其中所包含的边数
- 大多数情况下,我们研究的都是简单环和简单路径并会省略掉**简单**二字
- 当允许重复的顶点时,我们指的都是**一般**的路径和环
- 当两个顶点之间存在一条连接双方的路径时,我们称一个顶点和另一个顶点是**连通**的
- **无环图**是一种不包含环的图
- **树**是一幅无环连通图。互不相连的树组成的集合称为**森林**。连通图的**生成树**是它的一幅子图,它含有图中的所有顶点且是一棵树
- 图的**生成树森林**是它的所有连通子图的生成树的集合

- 图的**密度**是指已经连接的顶点对占所有可能被连接的顶点对的比例
- 在**稀疏图**中,被连接的顶点对很少;而在**稠密图**中,只有少部分顶点对之间没有边连接
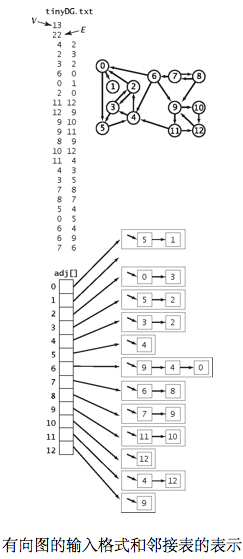
- 如下图中,V=顶点数,E=边数

- **二分图**是一种能够将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分
- 看下图例子,即每条边的两个顶点颜色不一样,分属不同的集合

- 无向图的数据表示
- 无向图的API

- 最常用的图处理代码

- 图的几种表示方式
- 基本要求
- 它必须为可能在应用中碰到的各种类型的图预留出足够的空间
- Graph的实例方法的实现一定要快——它们是开发处理图的各种用例的基础
- 方案
- **邻接矩阵**。我们可以使用一个V乘V的布尔矩阵。当顶点v和顶点w之间有相连接的边时,定义v行w列的元素值为true,否则为false
- 这种表示方法不符合第一个条件——含有上百万个顶点的图是很常见的,V^2个布尔值所需的空间是不能满足的
- 无法表示平行边
- **边的数组**。我们可以使用一个Edge类,它含有两个int实例变量
- 这种表示方法很简洁但不满足第二个条件——要实现adj()需要检查图中的所有边
- **邻接表数组**。我们可以使用一个以顶点为索引的列表数组,其中的每个元素都是和该顶点相邻的顶点列表,参见下图
- 这种数据结构能够同时满足典型应用所需的以上两个条件,我们会在本章中一直使用它

- 性能:
- 使用的空间和V+E成正比
- 添加一条边所需的时间为常数
- 遍历顶点v的所有相邻顶点所需的时间和v的度数成正比(处理每个相邻顶点所需的时间为常数)
- **边的插入顺序决定了Graph的邻接表中顶点的出现顺序**

- graph数据类型
- 这份Graph的实现使用了一个由顶点索引的整型链表数组。每条边都会出现两次,即当存在一条连接v与w的边时,w会出现在v的链表中,v也会出现在w的链表中


- 典型Graph实现的性能复杂度

- 图的处理算法的设计模式
- 需要设计search方法:找到和起点s连通的所有顶点
- 第一章的union-find算法是一种实现
- 设计marked方法:判断v和s是联通的吗
- 设计count方法:计算与s联通的顶点数

<!-- more -->
- 深度优先搜索算法(DFS)
- 迷宫的Tremaux搜索
- 选择一条没有标记过的通道,在你走过的路上铺一条绳子
- 标记所有你第一次路过的路口和通道
- 当来到一个标记过的路口时(用绳子)回退到上个路口
- 当回退到的路口已没有可走的通道时继续回退
- 绳子可以保证你总能找到一条出路,标记则能保证你不会两次经过同一条通道或者同一个路口

- 深度优先搜索(DFS)
- 要搜索一幅图,只需用一个递归方法来遍历所有顶点
- 将它标记为已访问
- 递归地访问它的所有没有被标记过的邻居顶点

- 单向通道
- 在Tremaux搜索中,要么是第一次访问区别了边的遍历方向的画法一条边,要么是沿着它从一个被标记过的顶点退回
- 在无向图的深度优先搜索中,在碰到边vw时,要么进行递归调用(w没有被标记过),要么跳过这条边(w已经被标记过)
- 顶点2是顶点0之后第一个被访问的顶点,因为它正好是0的邻接表的第一个元素
- 深度优先搜索中每条边都会被访问两次,且在第二次时总会发现这个顶点已经被标记过

- 深度优先搜索的详细轨迹

- 寻找路径
- 构造函数接受一个起点s作为参数,计算s到与s连通的每个顶点之间的路径

- 实现方式
- 记住每个顶点到起点的路径,而不是记录当前顶点到起点的路径
- 在由边v-w第一次访问任意w时,将edgeTo[w]设为v来记住这条路径。换句话说,v-w是从s到w的路径上的最后一条已知的边
- 类似于union-find算法,在到达s之前,将遇到的所有顶点都压入栈中。将这个栈返回为一个Iterable对象帮助用例遍历s到v的路径
- edgeTo[w]=v表示v-w是第一次访问w时经过的边。edgeTo[]数组是一棵用父链接表示的以s为根且含有所有与s连通的顶点的树


- 广度优先搜索算法(BFS)
- 深度优先算法无法解决找出某个点到起始点的最短路径
- **从s开始,在所有由一条边就可以到达的顶点中寻找v,如果找不到我们就继续在与s距离两条边的所有顶点中查找v,如此一直进行**

- 相比深度优先算法,**使用(FIFO,先进先出)队列来代替栈(LIFO,后进先出)即可**(从实现上来说,这几乎就是唯一的区别)
- 先将起点加入队列,然后重复以下步骤直到队列为空
- 取队列中的下一个顶点v并标记它
- 将与v相邻的所有未被标记过的顶点加入队列


- 代码实现

- 和深度优先搜索一样,一旦所有的顶点都已经被标记,余下的计算工作就只是在检查连接到各个已被标记的顶点的边而已
- 具体问题解决
- 连通分量
- 问题描述:给定一副图,找出其中相连的顶点,如1-2-3-4相连,7-8相连,则输出两组数据,1-2-3-4和7-8
- 具体实现
- 深度优先算法
- 使用了marked[]数组来寻找一个顶点作为每个连通分量中深度优先搜索的起点
- 第一次调用的参数是顶点0——它会标记所有与0连通的顶点
- 然后构造函数中的for循环会查找每个没有被标记的顶点并递归调用dfs()来标记和它相邻的所有顶点
- 另外,它还使用了一个以顶点作为索引的数组id[],将同一个连通分量中的顶点和连通分量的标识符关联起来(int值)
- 这里,标识符0会被赋予第一个连通分量中的所有顶点,1会被赋予第二个连通分量中的所有顶点,依此类推


- union-find算法
- 具体实现见第一章
- 和深度优先算法的比较
- 理论上,深度优先搜索更快,因为它能保证所需的时间是常数而union-find算法不行
- 实际应用中还是union-find算法更快
- 不需要完整地构造并表示一幅图
- union-find算法是一种动态算法(我们在任何时候都能用**接近常数**的时间检查两个顶点是否连通,甚至是在添加一条边的时候)
- 判断一个图是否是无环图
- 问题描述:给定一副图,假设不存在自环和平行边,判断该图不存在环(**环**是一条至少含有一条边且起点和终点相同的路径)

- 判断一个图是否是二分图(又称双色问题)
- 问题描述,给定一副图,能够用两种颜色将图的所有顶点着色,使得任意一条边的两个端点的颜色都不相同吗

- 符号图
- 处理字符串形式的顶点
- 定义输入
- 顶点名为字符串
- 用指定的分隔符来隔开顶点名(允许顶点名中含有空格)
- 每一行都表示一组边的集合,每一条边都连接着这一行的第一个名称表示的顶点和其他名称所表示的顶点
- 顶点总数V和边的总数E都是隐式定义的

- 二分图可以实现反向索引(?)TODO
- 举例来说,用电影名查到演员是正向索引,那么用演员查到电影名就是反向索引
- 实现
- 用到了以下3种数据结构
- 一个符号表st,键的类型为String(顶点名),值的类型为int(索引)
- 一个数组keys[],用作反向索引,保存每个顶点索引所对应的顶点名
- 一个Graph对象G,它使用索引来引用图中顶点

- 间隔的度数问题(?)TODO
- 有向图
- 术语定义
- 一幅有方向性的图(或有向图)是由一组顶点和一组有方向的边组成的,每条有方向的边都连接着有序的一对顶点
- 我们称一条有向边由第一个顶点指出并指向第二个顶点
- 一个顶点的出度为由该顶点指出的边的总数
- 一个顶点的入度为指向该顶点的边的总数
- 一条有向边的第一个顶点称为它的头,第二个顶点则被称为它的尾
- 在一幅有向图中,有向路径由一系列顶点组成,对于其中的每个顶点都存在一条有向边从它指向序列中的下一个顶点
- 有向环为一条至少含有一条边且起点和终点相同的有向路径
- 简单有向环是一条(除了起点和终点必须相同之外)不含有重复的顶点和边的环
- 路径或者环的长度即为其中所包含的边数
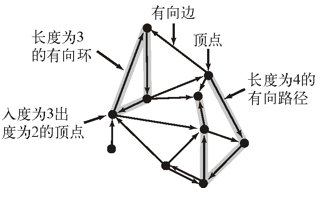
- 有向图的数据类型
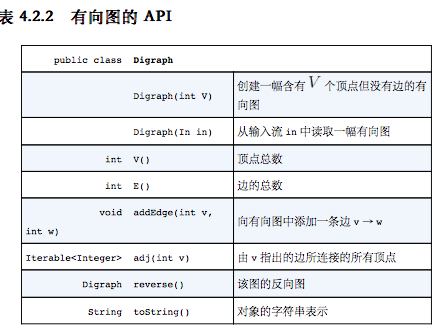
- 有向图的API
- Digraph的API中还添加了一个方法reverse()。它返回该有向图的一个副本,但将其中所有边的方向反转
- 有向图的表示:我们使用邻接表来表示有向图,其中边v→w表示为顶点v所对应的邻接链表中包含一个w顶点
- Digraph数据类型与Graph数据类型基本相同,**区别是addEdge()只调用了一次add()**,而且它还有一个reverse()方法来返回图的反向图

- 有向图的可达性
- 单点可达性。给定一幅有向图和一个起点s,回答“是否存在一条从s到达给定顶点v的有向路径?”等类似问题。
- 多点可达性。给定一幅有向图和顶点的集合,回答“是否存在一条从集合中的任意顶点到达给定顶点v的有向路径?”等类似问题。

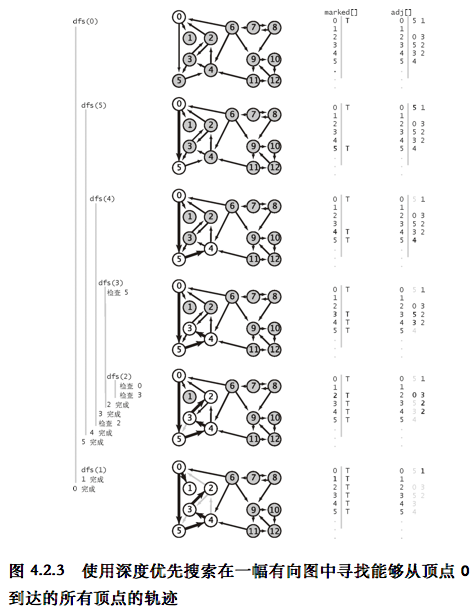
- DirectedDFS使用了解决图处理的标准范例和标准的深度优先搜索来解决这些问题。它对每个起点调用递归方法dfs(),以标记遇到的任意顶点。
- 使用深度优先搜索在一幅有向图中寻找能够从顶点0到达的所有顶点的轨迹


- 标记清除的垃圾收集
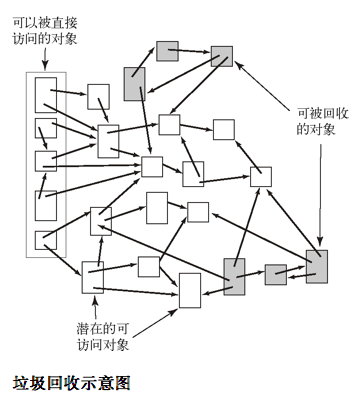
- 在一幅有向图中,一个顶点表示一个对象,一条边则表示一个对象对另一个对象的引用
- 程序执行的任何时候都有某些对象是可以被直接访问的,而不能通过这些对象访问到的所有对象都应该被回收以便释放内存
- 标记清除的垃圾回收策略会为每个对象保留一个位做垃圾收集之用
- 环和有向无环图
- 调度问题
- 优先级限制:它指明了哪些任务必须在哪些任务之前完成。不同类型的限制条件会产生不同类型不同难度的调度问题
- 优先级限制下的调度问题
- 给定一组需要完成的任务,以及一组关于任务完成的先后次序的优先级限制。在满足限制条件的前提下应该如何安排并完成所有任务
- 转换成有向图的问题描述:给定一幅有向图,将所有的顶点排序,使得所有的有向边均从排在前面的元素指向排在后面的元素(或者说明无法做到这一点)
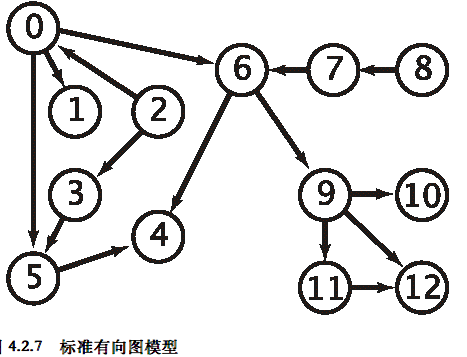
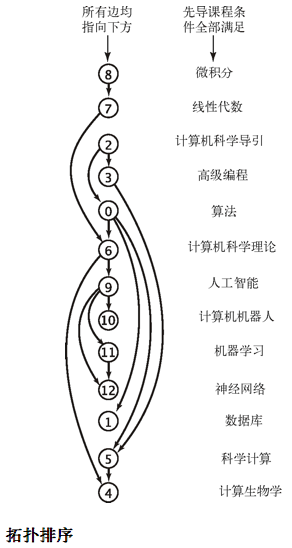
- 一般来说,如果一个有优先级限制的问题中存在有向环,那么这个问题肯定是无解的
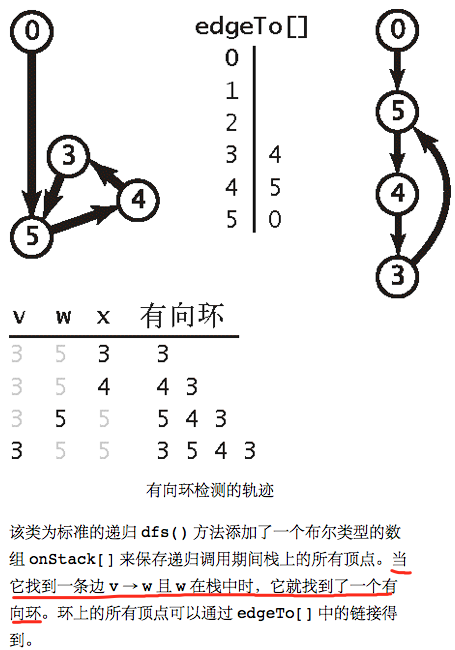
- 一旦我们找到了一条有向边v→w且w已经存在于栈中,就找到了一个环,因为栈表示的是一条由w到v的有向路径,而v→w正好补全了这个环

- 拓扑排序
- 当且仅当一幅有向图是无环图时它才能进行拓扑排序
- 拓扑排序的API

- 前序:在递归调用之前将顶点加入队列
- 后序:在递归调用之后将顶点加入队列
- 逆后序:在递归调用之后将顶点压入栈

- 一幅有向无环图的拓扑顺序即为所有顶点的逆后序排列
- 强连通性
- 如果两个顶点v和w是互相可达的,则称它们为强连通的,注意和无向图的区别
- 如果一幅有向图中的任意两个顶点都是强连通的,则称这幅有向图也是强连通的
- 强连通性将所有顶点分为了一些等价类,每个等价类都是由相互均为强连通的顶点的最大子集组成的。我们将这些子集称为强连通分量
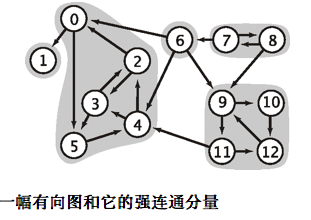
- Kosaraju算法(?)TODO
// 待续 TODO

















